[TeledyneLeCroy] "실시간 오실로스코프에서의 주파수 분석에 필요한 여섯 가지 원칙" 포스팅 업데이트
- 2022-08-08
- 조회수2422
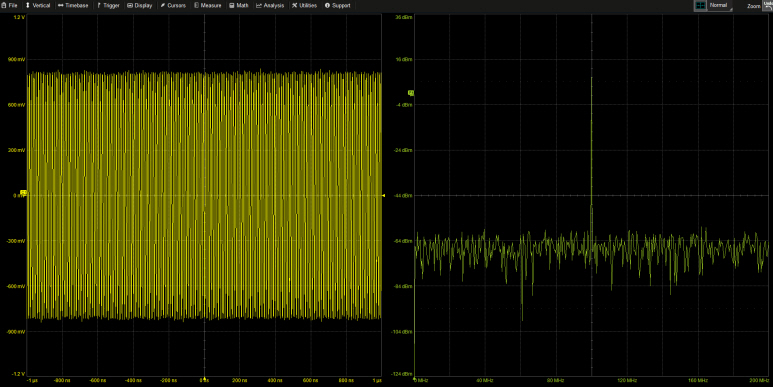
그림 1. 시간 도메인에서 100MHz 사인파와 주파수 도메인에서 하나의 피크로 나타난 스펙트럼.
우리는 시간 도메인 살고 있습니다. 모든 디지털 성능을 타임 도메인에서 측정합니다. 그러나 주파수 도메인으로 우회해보면 더 빨리 답을 얻을 수 있습니다. 이 블로그에서 말씀드리는 여섯 가지 원칙을 통해 오실로스코프가 시간 도메인 측정을 주파수 도메인에서 관측하는 화면으로 어떻게 변환하는 지를 이해할 수 있습니다. 여섯 가지 원칙 모두 FFT 기능이 내장되어 있는 오실로스코프와 SPECTRUM-1 및 SPECTRUM-PRO-2R 옵션과 같은 스펙트럼 분석을 위해 디자인된 소프트웨어 패키지의 내부에서 모두 적용되는 것들 입니다.
1. 스펙트럼은 사인파 성분의 조합입니다.
주파수 도메인에서 우리가 고려할 수있는 유일한 파형은 사인파입니다. 르장드르 다항식(Legendre polynomials), 에르미트 다항식(Hermite polynomials) 또는 웨이브릿과 같은 시간 도메인에서 파형을 설명 가능한 조합의 다른 특수 파형들이 있습니다. 주파수 도메인 설명을 위해 사인파를 골라내는 이유는 사인파가 저항, 커패시터 및 인덕터 요소와 관련된 전기 회로에서 자주 나타나는 방정식 인 2 차, 선형, 미분 방정식에 대한 해결책이기 때문입니다. 즉, RLC 회로에서 발생하거나 상호 작용에 의해서 사인파가 자연적으로 발생하기 때문에 다른 함수를 사용하는 것보다 사인파의 조합을 사용할 때 더 간단하게 설명할 수 있기 때문입니다.
그림 1은 사인파를 오실로스코프에서 1백만 개 데이터 포인트 메모리를 이용하여 포착한 전압-시간[V(t)] 데이터를 주파수 도메인에서는 3 가지의 숫자를 통해 설명하고 있습니다. 주파수 값, 진폭 값 그리고 위상 값이 바로 그 3 가지 정보입니다. 파형이 나타내는 정보를 아주 단순화했습니다.
2. 파형을 무한히 추가하면 주기적인 파형이 생성됩니다.
시간 도메인의 파형을 주파수 도메인으로 변환 하면 결국 주파수, 진폭, 위상을 가진 사인파들의 조합을 얻게 됩니다. 시간 도메인에서는 측정 값을 파형을 포착한 전체 시간 T, 샘플과 샘플 사이의 시간 간격인 ΔT를 가지고 있는 포착 메모리 버퍼로 기술합니다. 같은 파형을 주파수 도메인에서 기술할 때는 주파수, 진폭 및 위상을 가진 모든 사인파 구성 성분의 조합을 스펙트럼이라고 부릅니다.
아쉽게도 이산 푸리에 변환(DFT)은 연속적이고 주기적인 V(t) 파형에만 적용할 수 있습니다. 비주기적인 신호의 경우 인위적으로 주기적인 것으로 만들어줘야 합니다. 측정 된 데이터의 임의의 샘플 데이터를 주기적 파형으로 변환하는 데 사용하는 방법은 전체 시간 T의 메모리 버퍼가 그 이전과 이후에 영원히 반복하는 것입니다.
이렇게 인위적으로 반복되는 파형을 가지게 되면, DFT의 위력를 적용하여 스펙트럼 상의 주파수 성분을 수학적으로 계산할 수 있습니다. 다음은 각 주파수 성분의 진폭과 위상을 계산하는 데 사용되는 수식입니다.
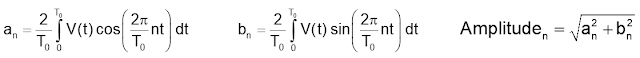
이 적분은 스펙트럼에서 특정하고 고유한 정보를 나타냅니다.
3. 스펙트럼에는 이산 주파수만 나타납니다. 가장 낮은 것이 기본성분입니다.
계산된 스펙트럼에서는 이산 주파수 값만 나타납니다. 가장 낮은 주파수 구성 요소를 기본 성분라고합니다. 포착 메모리 버퍼에 넣을 수 있는 가장 낮은 사인파의 주파수입니다. 가장 낮은 주파수의 사인파 주기 P는 전체 포착 시간 T와 같습니다.
따라서 주기 P가 전체 시간 T와 같으면 기본 주파수는 다음과 같습니다.
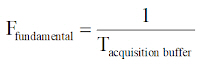
스펙트럼 상의 각 주파수 성분은 기본파의 정수배인 주파수 값을 갖습니다.
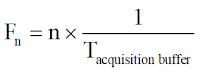
스펙트럼에서 볼 수 있는 주파수 구성 성분들은 오직 기본 성분의 배수들입니다. 즉, 각 주파수 구성 요소 사이의 주파수 간격 또는 분해능이 기본 주파수입니다. 스펙트럼에서 더 작은 주파수 특성을 구분해야 한다면 더 높은 주파수 분해능이 필요하며, 오실로스코프에서 포착 시간이 더 길어져야 합니다.
4. 가장 높은 주파수는 나이퀴스트 주파수 또는 샘플 속도의 반(1/2)입니다.
스펙트럼에서 확인할 수 있는 가장 높은 주파수 성분은 메모리에 샘플링되어 저장된 포인트들 사이의 간격과 연관되어 있습니다. 특정 주파수 성분의 진폭과 위상에 대한 값을 계산하려면 최소한 해당 주기에 두 개의 샘플 포인트 V(t)가 필요합니다. 이것은 우리가 계산할 수있는 가장 높은 주파수 성분을 갖는 사인파의 주기가 샘플링 간격의 두 배 또는 Pmax = 2 x ΔT라는 것을 의미합니다.
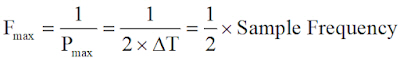
스펙트럼에서 가장 높은 주파수 성분을 나이퀴스트 주파수라고도 합니다. 데이터를 포착하기 위한 샘플링 속도는 1/ΔT이고, 사인파 성분을 계산할 수 있는 가장 높은 주파수는 나이퀴스트 주파수으므로 샘플링 속도의 절반입니다. 샘플링 속도가 10GS/s라면, 나이퀴스트 주파수는 5GHz입니다.
이상적인 사인파의 평균값은 항상 0입니다. 즉, 실제 파형을 표현하기 위해 사인파 조합을 사용한다면 재구성된 시간 도메인 파형의 평균 값은 항상 0입니다. 하지만 실제 파형에는 평균 값 또는 DC 오프셋이 있습니다. 이를 고려하여 DC 구성 요소를 0Hz 주파수 구성 성분으로 저장하며, 이것은 (기본 성분 x 0) 입니다. 대부분의 오실로스코프에서는 0번째 주파수 구성 요소를 플로팅하지 않도록 억제하여 디스플레이 되는 다이나믹 범위를 줄입니다.
5. FFT는 메모리의 데이터를 2^n 샘플 포인트로 짧게하여 계산 속도를 높입니다.
백만 개의 데이터 포인트를 이용하여 하나의 스펙트럼을 생성하려면 약 1 조 DFT 계산을 수행합니다. 이 문제를 해결하기 위해 FFT(Fast Fourier Transform)라는 훨씬 빠른 버전의 DFT를 사용합니다. DFT와 동일한 적분을 계산하지만 행렬 수학을 적용하여 2의 n제곱 개의 데이터를 사용하여 계산을 수행합니다. 메모리에 1백만 개의 데이터 포인트가 있는 경우 FFT 계산에 포함될 수 있는 가장 높은 포인트 수는 2^19 = 524,288포인트가 됩니다. 엄청나게 빠른 계산 시간을 얻기 위해 포착된 데이터의 거의 반을 버립니다.
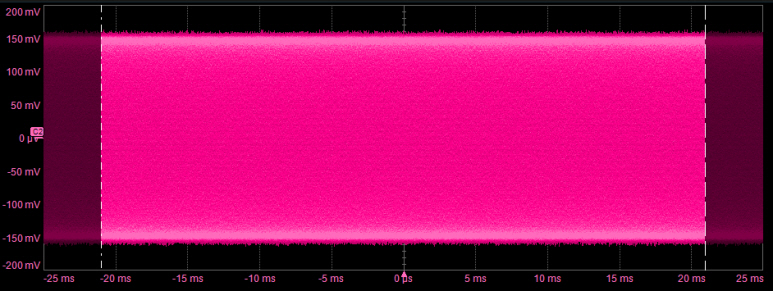
그림 2. 화면에 보이는 두 개의 수직축 마커 안에 있는 샘플이 현재 화면에서 FFT로 변환되는 2^n 개의 데이터입니다. 마커 밖에 존재하는 샘플들은 메모리에 존재하지만 FFT 연산에 사용하지 않습니다.
FFT를 수행하는 첫 번째 단계는 계산될 2^n 개의 데이터 포인트를 포함하는 영역을 설정하는 것입니다. 대부분의 오실로스코프를 사용하면 시간 도메인 화면의 가운데 부분 또는 왼쪽 끝에서 카운트 하도록 선택할 수 있습니다. 그림 2는 화면에서 강조 표시된 FFT 계산에 포함될 영역을 나타낸다.
신호를 포착한 전체 길이(시간)이 1μs이고 1백만 샘플 포인트가 있는 경우라면, 기본 주파수 성분, 즉 분해능,은 1MHz가 될 것으로 예상할 수 있습니다. 스펙트럼에서 FFT에 사용하는 샘플링 수는 신호 포착한 전체 데이터 보다는 적으며, 이것은 실제 스펙트럼 결과에 보이는 분해능은 1MHz 보다는 클 것이라는 것을 알 수 있습니다. 하지만 이 계산에의한 스펙트럼상의 특성을 생각해보면 여전히 유효한 사용하기에 부족하지 않은 값입니다.
6. 윈도우 함수는 데이터 축소에의한 스펙트럼 누출을 방지합니다.
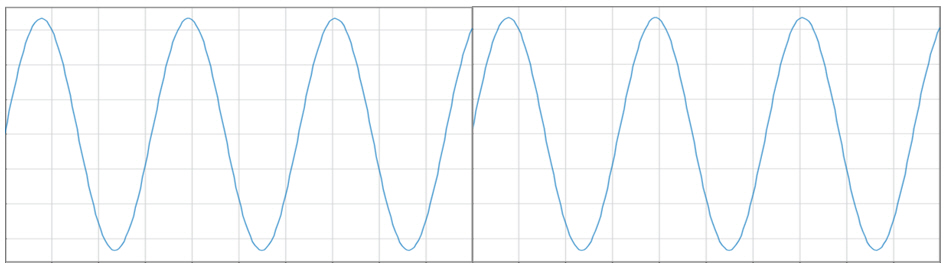
그림 3. 포착 메모리에 정수배의 사이클 수를 갖지 않는 사인파의 예, 연속파로 만들어진 부분에서 파형의 불연속성이 존재합니다. (이미지 : 내셔널 인스트루먼트)
주기적이고 연속 파형을 생성하기 위해 메모리의 데이터를 가져와 무한이 반복했습니다. FFT 연산을 수행할 때 포착 메모리를 추가적으로 2^n 제곱의 데이터 개수로 만들기위해 추가적으로 축소시켰고, 해당 샘플들은 반복했습니다. 즉, 추가되는 메모리의 시작과 끝이 만나는 경계점의 파형에 불연속이 발생할 수 있습니다(그림 3).
일반적으로 정수배의 사이클 수를 갖는 사인파의 스펙트럼은 피크 주파수에서 단일 스파이크를 갖습니다. 그러나, 사인파가 잘린 포착 부분으로 인해 인위적으로 잘려진 경우, 생성된 무한히 긴 연속 파형에는 이제 주파수 성분중 일부를 피크 주파수에 인접한 주파수 성분으로 강제하는 불연속성을 갖게 되어 왜곡이 발생할 수 있습니다.
이 효과를 스펙트럼 누출이라고합니다. 첫 번째 전압 값이 마지막 전압 값과 동일하지 않기 때문에 데이터가 연결되는 경계에서 불연속성에 의한 인공적으로 발생한 것입니다. 이 누출울 줄이는 방법은 전체 메모리 버퍼에 윈도우 함수를 곱하여 인위적으로 불연속성을 줄이는 것입니다. 이렇게 하면 획득 버퍼의 끝에 있는 전압 값이 점차 0에 가까와 지고 데이터의 끝이 다음 메모리 데이터의 시작부분과 연속이 될 수있도록 보장합니다.
일반적으로 사용되는 여러 가지 윈도우 함수가 있습니다. 적용한 윈도우에 따라 얼마나 많은 스펙트럼 누출을 허용하는 지와 결과에서의 분해능이 다릅니다. 특정 윈도우를 사용해야 할 특별한 이유가 없다면, 항상 von Hann (Hanning이라고도 함) 또는 Blackman-Harris 함수를 사용하는 것이 좋습니다.
주파수 도메인에서 시간 도메인 파형 분석
스펙트럼 분석을 통해 주파수 분해능 (1/포착 시간)과 나이퀴스트 (1/2 x 샘플링 속도) 사이의 범위에 맞는 주파수로 반복적인 신호의 스펙트럼 특성을 파악할 수 있습니다. 오실로스코프가 시간 도메인에서 전압 또는 크기 정보를 포착하여 메모리가 업데이트 될 때마다 새로 계산된 스펙트럼 응답 결과가 화면에 표시됩니다. 소스 신호의 주기 정보가 변경되면, 스펙트럼 상에서의 주파수에 대한 고유한 정보 또한 변경됩니다.
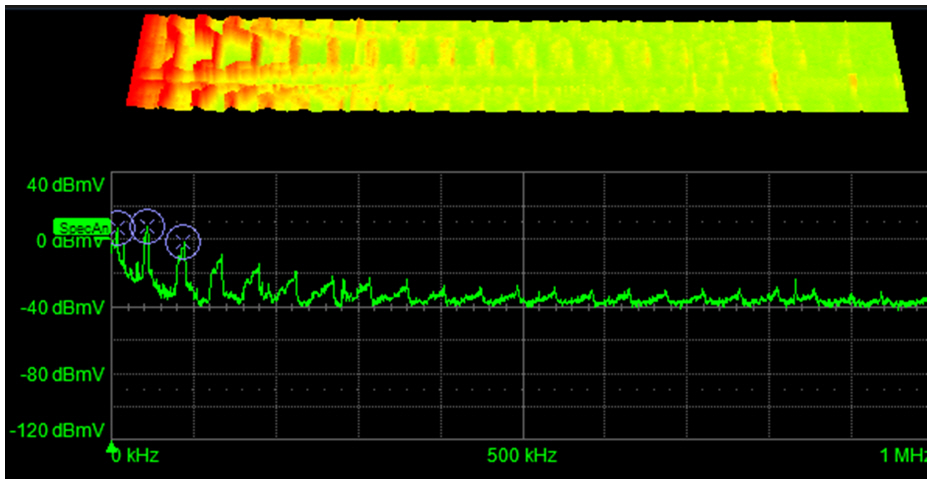
그림 4. 출력 부하가 변경되는 상황에서 포착한 SMPS 출력의 실시간 스펙트럼은 피크 주파수가 시간에 따라 변하는 정보를 바로 나타냅니다.
주어진 주파수 범위에서 주기적인 신호를 식별하는 것이 필요한 모든 애플리케이션에서 실시간 스펙트럼 분석은 훌륭한 솔루션을 제공하는 후보입니다. 가장 일반적으로 적용되는 예는 중요한 신호에 영향을 주는 간섭원을 찾아내는 것입니다. 그림 4는 부하가 변경되었을 때 스위치 모드 전원 장치(SMPS)의 출력에 대한 스펙트럼 응답을 보이고 있습니다. 스위칭 주파수인 약 50kHz에서의 피크가 그림의 위부분에 보이고 있는 스펙트로그램에서 확인할 수 있는 것 처럼 부하의 변동에 따라 그 주파수도 시간에 따라 변하고 있습니다. 증폭기의 잡음 또는 오실레이터의 지터에서 이런 주파수 성분을 관측함으로써 영향을 줄 수 있는 근본 원인을 찾을 수 있는 아이디어를 제공합니다.
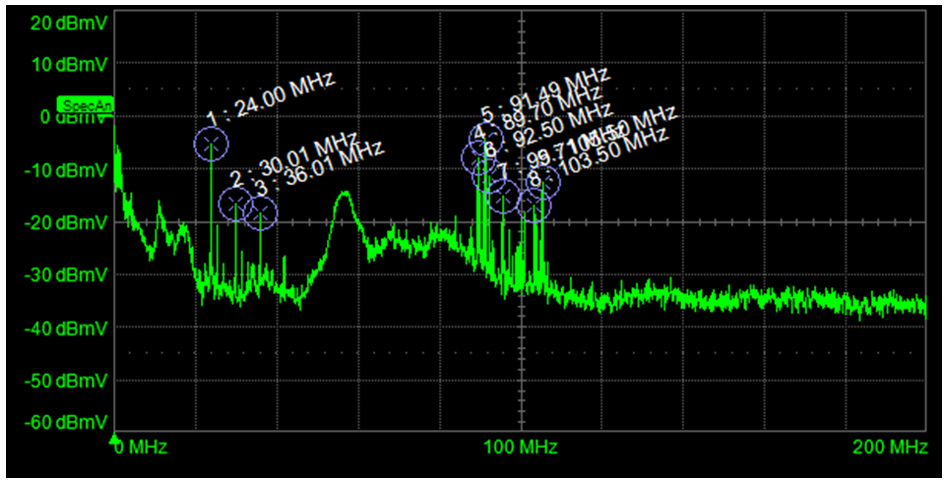
그림 5. USB 전원 레일에서의 노이즈를 실시간 스펙트럼을 측정하여, 프로브에서 픽업된 FM 라디오 대역의 주파수 성분을 보이고 있습니다.
RF 간섭의 스펙트럼을 볼 때, 우리는 종종 특정 통신 신호를 포착 할 수 있습니다. 그림 5는 크고 루프가 있는 10x 프로브를 사용하여 USB 전원의 파워 레일 신호를 포착하여 수행하고 있는 실시간 스펙트럼을 보이고 있습니다. 스펙트럼 상의 정보에서 87MHz ~ 108MHz의 FM 라디오 대역에서 신호가 픽업되고 있음을 알 수 있습니다.